고정 헤더 영역
상세 컨텐츠
본문
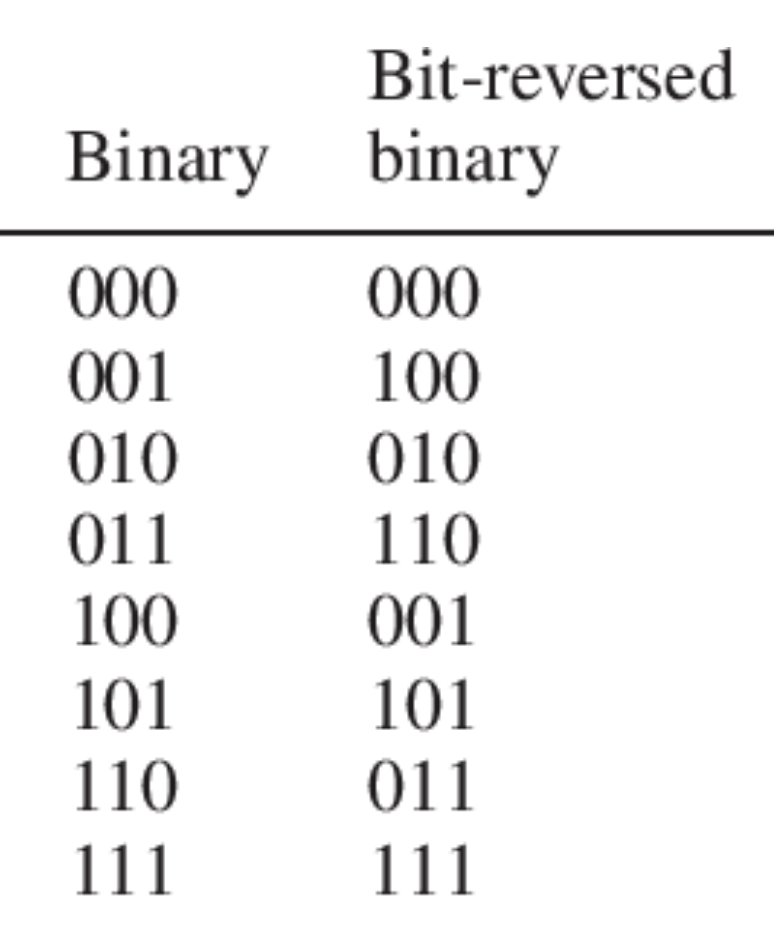
비트 연산 문제를 처음 접하면 익숙하지 않은 기호들 때문에 어렵게 느껴지지만, 한 번 감이 잡히면 굉장히 재미있는 카테고리다.
이번 글에서는 LeetCode 190번 문제인 Reverse Bits를 풀면서,
내가 처음 짠 풀이와 흔히 “정석 풀이”라고 불리는 접근법을 비교해본다.
https://leetcode.com/problems/reverse-bits/description/
📌 문제 요약
32비트 정수 n이 주어지면, 이 값을 이진수 비트 단위로 완전히 뒤집은 숫자를 반환하는 문제다.
예를 들어,
00000010100101000001111010011100
을 뒤집으면
00111001011110000010100101000000이 되고, 이 값을 다시 십진수로 바꾼 것이 정답이다.
✨ 내가 처음 생각한 풀이: 수학식 기반 접근
처음에는 비트를 하나씩 읽어서, “뒤집었을 때 그 비트가 있어야 하는 자리”를 구해
2^(31 - i)을 더하는 방식으로 해결했다.
public int ReverseBits(int n)
{
int answer = 0;
for (int i = 0; i < 32; i++)
{
answer += ((n >> i) & 1) * (int)MathF.Pow(2, 31 - i);
}
return answer;
}
🔍 이 풀이의 특징
- **“i번째 비트 → (31 - i)번째 자리”**라는 논리를 그대로 코드로 옮긴 형태
- 직관적이고 수학적으로 명확함
- 비트 문제를 처음 접한 사람이 떠올리기 좋은 접근
- 실제로도 문제는 완전히 맞게 풀 수 있다
⚠️ 단, 몇 가지 아쉬운 점
- MathF.Pow는 float 기반 계산이라 불필요하게 무겁다
- 2^31은 int 범위를 초과해서 캐스팅 시 int.MinValue가 되는데,
- 비트 패턴은 맞지만 코드를 읽는 사람에게 혼란을 줄 수 있음
- 매 반복마다 Pow 호출 → 코스트가 생김
- 비트 문제인데 float 연산이 등장해 의도가 흐려 보임
✨ 정석 풀이: 순수 비트 연산 기반 접근
비트 뒤집기는 결국 “비트를 하나씩 꺼내서 반대쪽 끝에 쌓는” 작업이다.
정석 풀이에서는 이를 비트 이동 연산 (<<, >>, |, &)만 사용해 구현한다.
public int ReverseBits(int n)
{
int answer = 0;
for (int i = 0; i < 32; i++)
{
answer <<= 1; // answer를 왼쪽으로 이동해 자리 확보
answer |= (n & 1); // n의 마지막 비트를 answer에 추가
n >>= 1; // n을 오른쪽으로 밀어 다음 비트를 준비
}
return answer;
}
🔍 이 풀이의 특징
- 비트를 하나씩 떼어내 순서대로 쌓는 방식, 문제의 본질과 딱 맞물린다
- float 연산 없이 순수 정수 비트 조작만 사용
- 캐리(carry) 발생 위험이 없다
- 면접/코딩테스트에서 가장 선호되는 “전형적인 비트 조작 패턴”
📚 마무리
비트 연산 문제는 처음엔 낯설지만,
이 문제처럼 한두 가지 패턴만 익혀도 금방 재밌어진다.
이번 문제를 통해:
- 비트를 위치 단위로 조작하는 방식
- 비트 이동의 의미
- OR(|=)와 덧셈(+)의 차이
- 비트 연산의 정석 패턴
을 한 번에 익힐 수 있었다.
'개발기록 > 자료구조 & 알고리즘' 카테고리의 다른 글
| 비트 연산으로 이해하는 2의 거듭제곱 - Math.Pow 대신 1 << n을 사용하는 이유 (0) | 2025.12.12 |
|---|---|
| LeetCode 136. SingleNumber — XOR 연산 응용 (0) | 2025.12.11 |
| LeetCode 191 — Number of 1 Bits (이진수에서 1 개수 세기) (0) | 2025.12.11 |
| 퀵정렬 원리 아주 쉽게 이해하기(Quick Sort) (0) | 2024.11.08 |
| 백준 1316 - 그룹 단어 체커 (파이썬) (0) | 2021.01.16 |




